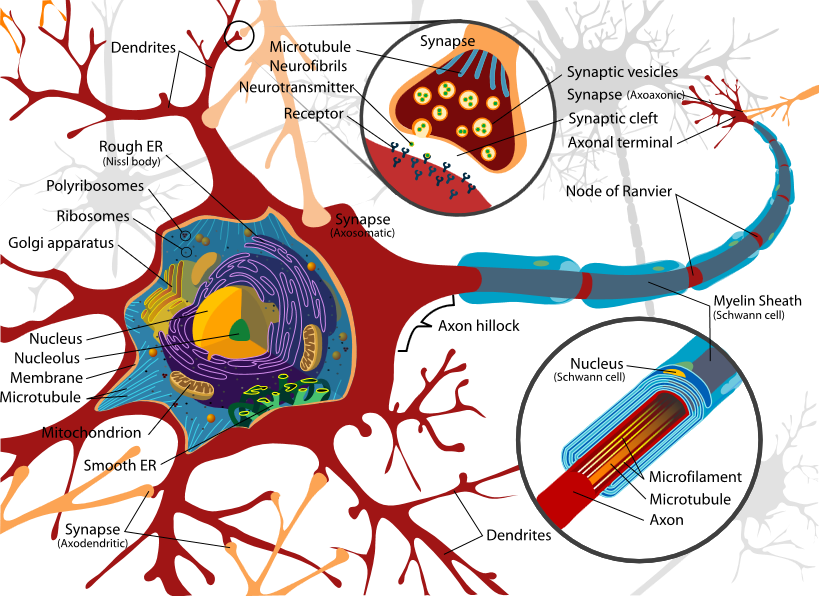
ニューラルネットワークは、動物の脳内で神経細胞が相互に接続している状態を、数学モデル化し、それをデジタル回路に実装したものです。ニューラルネットワーク機械学習の起源は、動物の脳細胞の解剖実験、つまり生物学にあります。
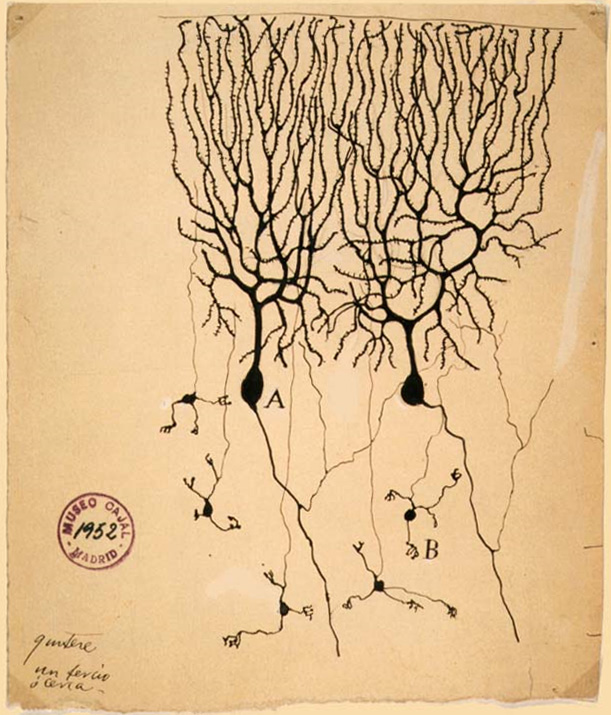
大脳皮質の神経細胞は、シナプスで相互に接続されており、個々の神経細胞は、シナプスから受領した電位を総計して一定レベルを超えると、隣の神経細胞に電位を伝達します。
例えば、人がAという文字を見たときは、Aという文字の個々の特徴点に選択的に反応する神経細胞が、過去にAを見た経験で学習した伝達経路を辿って脳のAという文字の記憶の目的地に伝達され、「Aを見ていますよ」と脳内に号外を出すわけですが、その時の神経細胞の伝達は、Aという文字に含まれる特徴を抽出する各細胞が、特徴を抽出したかどうかを隣の細胞に伝達することの繰り返しによって行われているわけです。文字認識の精度が向上すると、複雑で曖昧な手書き文字の認識もできるようになります。
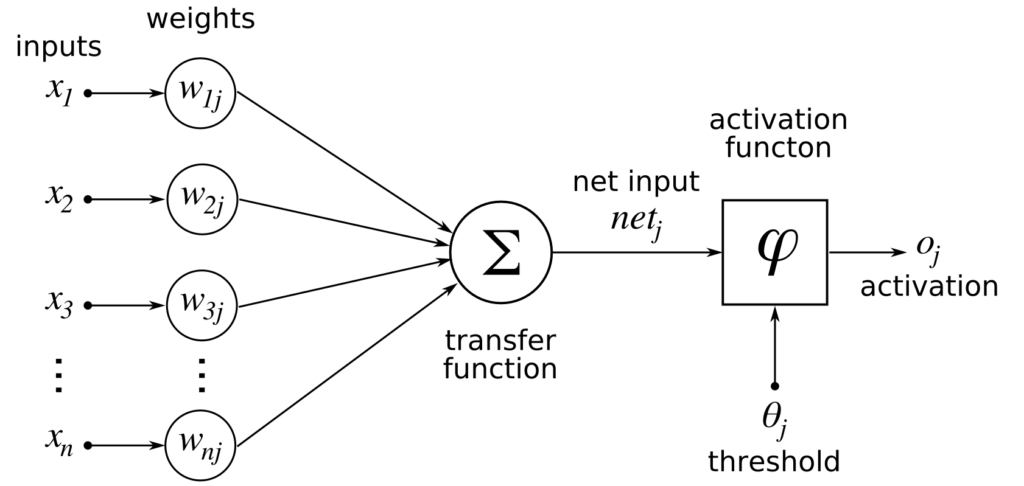
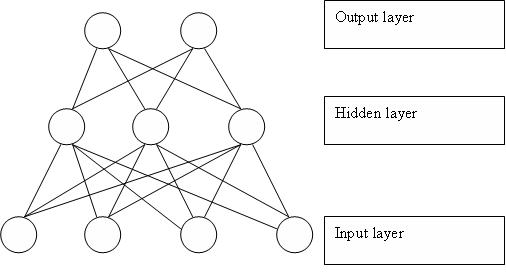
これと同じ事がコンピューター回路でも出来るのではないかと考えたのが、アメリカの心理学者・計算機科学者フランク・ローゼンブラットです。彼はモデル神経細胞(形式ニューロン)が3層から成る、認識計算機を考案し、1958年にパーセプトロンとして論文発表しました。与えられたデータを近似する識別関数が正しいかどうか確認して、誤りがあれば識別関数のパラメータを少し修正して再確認することを繰り返す学習規則(固定増分誤り訂正法)により、正しい識別関数(近似関数)を獲得することができます。これは統計学における線形回帰、線形近似関数(線形識別関数)を求めることと同義であると評価できます。データから特徴を抽出するパターン認識と、統計学の近似関数を求める回帰分析とは同じことなのです。
パーセプトロンは後に数学的に、2クラス問題(2種類のデータを分類する問題)が1次関数で分離できる場合(線形分離可能な場合)のみ適用できると証明されました。パーセプトロンの能力と限界が明かになったわけですが、それは機械学習の改良の前兆でもありました。
https://ja.wikipedia.org/wiki/パーセプトロン
※image from wikimedia
スウェーデンの神経科学者トルステン・ウィーセルと、カナダの神経生理学者デイヴィッド・ヒューベルは、1959年に、麻酔したネコの大脳視覚野に微小電極を刺入し、眼前に置いたスクリーンに様々なパターンを映し出したときの視覚野ニューロン応答を調べ、ある特定の方向の棒状刺激に対してスパイク応答を示すが別の角度に対しては発火しない細胞があることを発見しました。その後の研究で、刺激提示位置や方位に対して選択的に応じるニューロンどうしが規則的なルールに従って視覚野を形成していることなどを発見し、単純な刺激が複雑な像となって表れる視覚の仕組みが明らかになり、1981年ノーベル生理学医学賞を受賞しました。
日本の福島邦彦は、ヒューベルとウィーセルの実験から着想を得て、1979年にネオコグニトロンを開発しました。視覚神経モデルをコンピューターの文字認識に使えるようにする、計算モデルを開発したのです。これは「教師無し学習」によって画像の特徴を抽出し、ニューラルネットワークの重み付けを修正していくことにより文字認識の正解率を高めるというものでした。
http://personalpage.flsi.or.jp/fukushima/files/research.html
視覚のパターン認識に使えるということは、他の知覚(聴覚、嗅覚、触覚)や、概念理解(機械翻訳)にも使える可能性があるということになります。全ての情報はn次元の(任意の次元の)関数として数値化(抽象化)できますから、ニューラルネットワークにそれを入力すれば人間の知覚能力と同様の能力を獲得できることになります。多層ニューラルネットワークは多項式と同じで、任意の関数を近似表現することができます。
動物の脳の認識能力は、正解値と試行錯誤の誤差関数の最小値を取得する計算であり、微分方程式を解く(誤差関数の微分係数がゼロの地点を探す)ことと同じことですが、それは数式を解析学的に文字通り解く必要は無く、仮の答えと正解値を比較して、ニューラルネットワークを微調整して再度仮の答えを出して正解と比較することを繰り返すこと(勾配降下法)でも、正解に至ることはできるのです。勾配降下法の試行錯誤は、デジタルカメラのコントラスト検出AF方式にも似ている考え方です。どんな関数か分からなくても、とにかく正解との差が分かればOKということです。
イギリスのジェフリー・ヒントンは、ニューラルネットワークを改良させ、ディープラーニングの手法を確立させました。猫の脳の視覚野の多層構造をヒントに畳み込みニューラルネットワークが設計されました。畳み込み層では、畳み込みフィルターと呼ばれる小さな特徴検出器の発火の有無をニューラルネットワークの入力層に伝達します。
https://ja.wikipedia.org/wiki/ディープラーニング
ニューラルネットワークのアルゴリズムの改良と並行して、ムーアの法則による計算機の性能向上(2年で2倍)が作用し、画像認識、音声認識、自然言語理解(機械翻訳)の精度が劇的に進歩しました。2012年6月にグーグルが発表した論文いわゆる「キャットペーパー」では、ニューラルネットワークによる大規模な教師無し学習(16000コアの1000台のPCで3日間)によって、コンピューターが誰からも教えられずに、多数の猫画像を見ただけで、自力で猫を認識できるようになったことが明らかにされています。これは「グーグルの猫」と呼ばれ、ディープラーニングのひとつのマイルストーン(一里塚、通過点)と認識される出来事になりました。2012年は、ILSVRC画像認識コンテストでジェフリーヒントンらのディープラーニング画像認識エンジンが初優勝した記念すべき年でもあります。
※グーグル公式ブログより、「グーグルの猫」プレスリリース
https://googleblog.blogspot.jp/2012/06/using-large-scale-brain-simulations-for.html
※LSVRC説明
http://www.image-net.org/challenges/LSVRC/
その後、自動車の自動ブレーキ技術が対向車や、自転車や、歩行者を見分けることができるようになり、自動運転技術が進歩し、音声認識を活用したamazon echo(2014年11月)や google home(2016年11月) の発売に至っているわけです。2016年3月にグーグルの人工知能専門チーム「ディープマインド」が作った「AlphaGo (アルファ碁)」が、世界最高峰の棋士、韓国のイ・セドル氏に勝利しました。これは囲碁の棋譜を沢山読み込ませることによる機械学習で囲碁の能力を高めるという手法で、人間のプログラミングによって指し手の関数が造られたわけではないところが衝撃的でした。もうプログラマーは一切不要になると考えている計算機科学者も居ます。これをディープラーニング革命といい、モラベックのパラドックス(AIは知的作業は得意だが、幼児にもできる認識や物理的動作が苦手という主張)が覆りつつあると指摘されています。
AI囲碁のプログラムを開発した機械学習の専門家も、ニューラルネットの中でどのような計算が行われて、指し手が生成されているのか分かりません。ハンガリー出身の物理学者・社会哲学者マイケル・ポランニーが提出した「ポランニーのパラドックス」によれば、人は常に記述できない暗黙知を駆使しており、どこまで行っても記述できない部分が残るとされていましたが、ディープラーニングは、ポランニーのパラドクスを打破してしまったのかも知れません。
ディープラーニングによりAIが獲得した能力は、猫の認識とか、囲碁の能力だけに留まりません。人間の脳が行うあらゆる情報処理が、AIによって代替されうるということを意味します。しかもそのコストが日々低下してきているのです。これが社会に与えるインパクトがどれほど大きいか、正しく理解する必要があります。この問題は「労働を奪う」という側面が強調されがちですが、「労働が不要になる」という側面があることも良く考える必要があります。生産性が極限まで向上し、人間が関与せずに、あらゆる労働成果を得ることができる可能性があるということになります。
※参考書籍
タリクラシド、ニューラルネットワーク自作入門
涌井良幸・涌井貞美、ディープラーニングがわかる数学入門
斎藤康毅、ゼロから作るDeep Learning