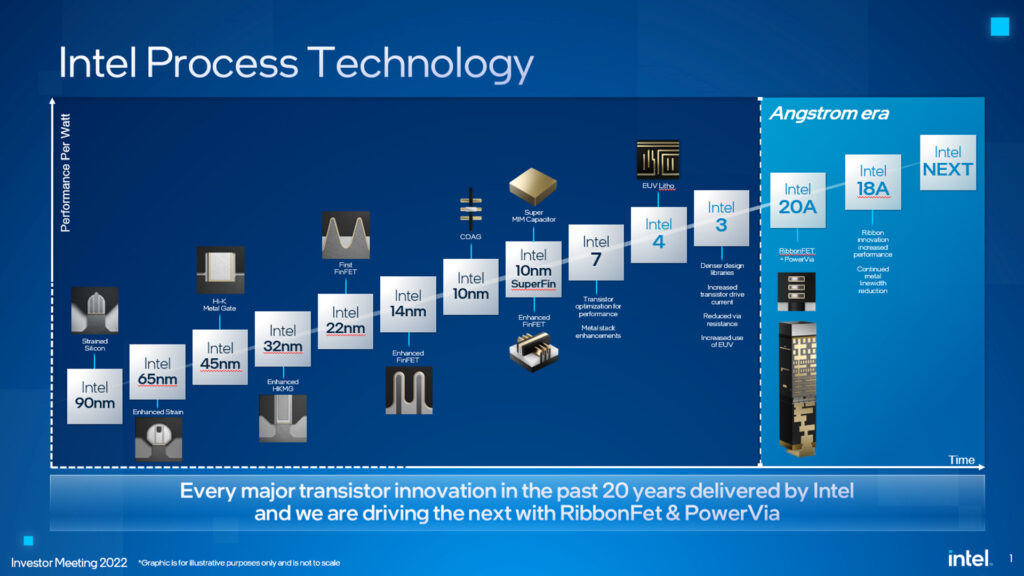
ムーアの法則とは、半導体プロセスの微細化により2年で2倍のトランジスタ数が搭載できるようになるという経験則です。
現在の主要CPUプロセスルール=3nm(2023年12月現在)
※apple A17 pro & M3
シリコン半導体は、シリコン=ケイ素=Siの単結晶に自由電子や自由正孔(電子が入る穴)を添加して高速スイッチとして動作させます。半導体回路は、円盤形のシリコン単結晶ウエハーに、銀塩写真のように回路を焼き付けて製造します。この焼き付ける機械が、半導体露光装置(ステッパー)です。この焼き付ける回路の最小分解能がプロセスルールです。どれだけ細い線をウエハーに印刷出来るか、という問題です。
ここで単位の勉強です。学習用定規に刻まれている最小単位は1ミリだと思いますが、1ミリの千分の1が、1ミクロン=1μmです。そして、そのまた千分の1が、1ナノメートル=1nm=10オングストロームです。ちなみに髪の毛の太さは1本80ミクロン程度、一般的なコピ-用紙の厚さも同程度です。
シリコン原子がジャングルジムのように並んでいるシリコン単結晶ウエハーにおいて、シリコン原子1個の大きさは0.222ナノメートル(2.22オングストローム)です。この数字は、地球上では、どんなに技術が進歩しても変わらない数値です。
2022年現在、スマホ心臓部にあるマイクロプロセッサ(SM8475)は、4nmのプロセスルールで製造されています。ウエハーに印刷される1本の線が、シリコン原子18個というレベルに到達しています。製造工程は台湾のTSMC、半導体露光装置はオランダのASMLです。
研究室レベルでは2ナノ露光も実現
IBMは2021年5月7日に世界初の2nm露光デバイスの試験に成功したと発表しています。2nmチップは指の爪のサイズのチップに最大500億個のトランジスターを搭載できるといいます。
ムーアの法則の歴史
フェアチェイルドとインテルの共同創立者ゴードン・ムーアは、1965年に、エレクトロニクス誌で発表した記事で、次のように述べています。半導体ウエハ上に形成されるトランジスタ部品の数が年に2倍になるという予測ですが、これは後日2年で2倍と修正されています。これは具体的な数値を持つ法則ではありますが、何ら科学的な根拠の無い「経験則」です。つまり、過去にこのように進歩してきたから将来も同じようなペースで進歩するかもしれない、ということです。
The complexity for minimum component costs has increased at a rate of roughly a factor of two per year (see graph on next page). Certainly over the short term this rate can be expected to continue, if not to increase. Over the longer term, the rate of increase is a bit more uncertain, although there is no reason to believe it will not remain nearly constant for at least 10 years. That means by 1975, the number of components per integrated circuit for minimum cost will be 65,000. I believe that such a large circuit can be built on a single wafer.
(和訳)最低費用(訳注=研究室実験レベルではなく半導体工場の実用レベルという意味)で製造できる部品の複雑さは、毎年約2倍のペースで増加してきた。確かに、当面の間、増加することは無いとしても、このペースは維持されると期待される。更に長期で言えば、この増加率が維持されるかどうかはやや不確実ではあるが、すくなくとも今後10年間はこの増加率を維持しないと考えない理由は無い。これは1975年頃までに最低費用で製造できる集積回路(IC)の部品数は6万5千(訳注=1965年当時が65個であったので2の10乗=1024倍して、約65000個と予測している)になることを意味する。私はこのような大きな回路がひとつの半導体ウエハ上に製造できると信じている(訳注=LSIの到来を予言していると言える)。
https://drive.google.com/file/d/0By83v5TWkGjvQkpBcXJKT1I1TTA/view
https://en.wikipedia.org/wiki/Moore%27s_law
デナード縮小則
ムーアの法則は、DRAMの発明者ロバート・デナードによるデナード縮小則(Denard scaling)とセットに考えられてきました。集積回路におけるMOSFETは微細化すればするほど性能が向上するという法則です。IEEE Journal of Solid State Circuits.1974年10月に次のような論文が掲載されています。
The principles of device scaling, show in a concise manner the general design trends to be followed in decreasing the size and increasing the performance of MOSFET switching devices.
(和訳)半導体デバイスの縮小法則は、MOSFETスイッチング素子のサイズを小型化するにつれ性能が向上するという設計傾向に簡潔に現れています。
http://www.ece.ucsb.edu/courses/ECE225/225_W07Banerjee/reference/Dennard.pdf
デナード則は2005年頃に終了したという意見もあります。漏れ電流の影響が無視できなくなり、CPUの駆動周波数を上げづらくなり、代わりにコア数を増やしたり拡張命令セットなどにより性能向上させる手法が増えてきました。
半導体露光装置最大手であるオランダのASMLは、EUV露光装置を改良し、3nm以降の微細化にも意欲を示しています。ベルギーのimecと共同でhigh NA euv research laboratory を設立しています。
https://www.imec-int.com/en/articles/imec-and-asml-enter-next-stage-of-euv-lithography-collaboration
ムーアの法則の終焉
しかし、露光装置の微細化はシリコン原子のサイズに肉薄しており、限界が近いという意見もあります。IC(集積回路)が発明されてから50年以上続いてきたムーアの法則がそんなに簡単に終わってしまうのでしょうか。少なくとも現在のLSIの製造方法を見る限り、「もうシリコン原子が見えるところまで到達して限界だ!」という意見には説得力があるものです。
ムーアの法則終焉・崩壊について参考URL
https://blogs.nvidia.com/blog/2017/05/10/live-jensen-huang-gpu-technology-conference-2017/
http://www.cspp.cc.u-tokyo.ac.jp/p-moore-201512/
しかし、これを覆す可能性のある技術が、いま、芽生えています。それは「3次元回路」です。ウエハーに回路を印刷したものを、何枚も重ねて繋ぐという技術で、フラッシュメモリの分野では一部実用化されており96層メモリが出荷されています。高層マンションにエレベーターが設置されているのと構造的には似ているものです。現在はフラッシュメモリ分野のみ実用化が進んでいますが、将来CPU分野にも3次元化の波が到来する可能性があります。
※Micron、176層NAND FLASH紹介ページ
https://investors.micron.com/news-releases/news-release-details-204
また、露光範囲の拡大によっても微細化と同じ効果を得ることができるかもしれません。いま、半導体露光装置は30ミリ四方の範囲を露光することができますが、もしも60ミリ四方の範囲を露光できるようになれば2倍の分解能で露光したのと同じ効果を得ることができます。「どうやってそんなことができるのだ?」あなたは言うかもしれませんが、そんなことは分かりません。それを世界中の研究者・技術者が毎日追求しているのです。
米国カリフォルニア州のcerebras systems は300ミリウエハ全面に1.2兆個のトランジスタを搭載したディープラーニング専用チップの開発に成功しています。
https://www.cerebras.net/wp-content/uploads/2019/08/Cerebras-Wafer-Scale-Engine-Whitepaper.pdf
System on a chip (SOC)という技術も毎年進化しています。これは集積回路の1個のチップ上にプロセッサコアの他にグラフィックエンジンやAD変換器やセンサーなど応用機能なども集積し、連携してシステムとして機能する集積回路製品です。アナログ回路とデジタル回路の混載も可能となっており、チップ上に設置できる部品の種類がどんどん増えています。極端に言えば、将来的にプリント基板が不要になる可能性すらあります。
モアザンムーア
このように微細化以外の方法による集積回路の高性能化を目指す取り組みは、モアザンムーア(More than Moore)と呼ばれています。AMDは RYZEN threadripper2 CPU で、4094ピンのSocket TR4に、半導体4個を搭載したCPUを接続して、32core 64thread の動作を可能にする改良を行いました。いわゆるSiP(system in a package、チップレット技術)というもので、これもモアザンムーアのひとつです。2022年3月にはチップレットの標準仕様を策定する業界団体UCIe(Universal Chiplet Interconnect Express)が設立されています。
ウエハーレベルCSP, Wafer-level packagingという技術もあります。半導体の出力端子を純金ワイヤボンディングで金属の端子に横方向に接続するのではなく、半導体を切り出したサイズのまま垂直に銅配線とハンダボールを設置する技術です。半導体そのもののサイズは同じでも、プリント配線基板に設置したときの実装密度が大幅に向上します。
LSIを実装するプリント基板の多層化・高密度化も恐るべきスピードで進展しています。
※デンソーの129層PCB基板
https://www.denso.com/jp/ja/news/other-topics/2013/130524-01.html
一般人には詳細は分からなくても、手段の如何を問わず、とにかくCPUの性能が倍々ゲームで向上している状況に変化は無いのです。
ポストムーア
ムーアの法則が限界を迎えた後の世界を「ポストムーア」と呼びます。半導体の進化が止まった後、というようなニュアンスがありますが、ムーアの法則とモアザンムーアが終わるということは明確なことではありません。半導体の進化は、石油の可採年数のようにどんどん延期されてきた歴史があります。進歩が鈍化したり停止するとしても、その時の半導体技術のパワーは2020年の我々には想像もできないレベルであると考えます。
ムーアの法則が社会全体に影響を与えている以上、「半導体なんて関係無い」という態度は許されません。半導体回路の微細化、3次元化、露光範囲の拡大、その他手法による集積度の向上は、日々進化していますから、我々も日々チェックして、将来どうなるか見つめていく必要があります。
※おまけ、スパコンTOP500の性能向上率
1993/11 Numerical Wind Tunnel Fujitsu,124 GFlops
2020/11 Supercomputer Fugaku, 442,010 TFlops
27年間の倍率は、442010 ÷ 0.124 = 3,564,596倍
この27乗根=1.7485倍、スパコンは毎年1.74倍に計算速度が上昇しています。これはムーアの法則の2年で2倍、つまり1年でルート2=1.41倍よりも大きな数値です。ムーアの法則が終わることなんて関係無いわけです。
量子版ムーアの法則
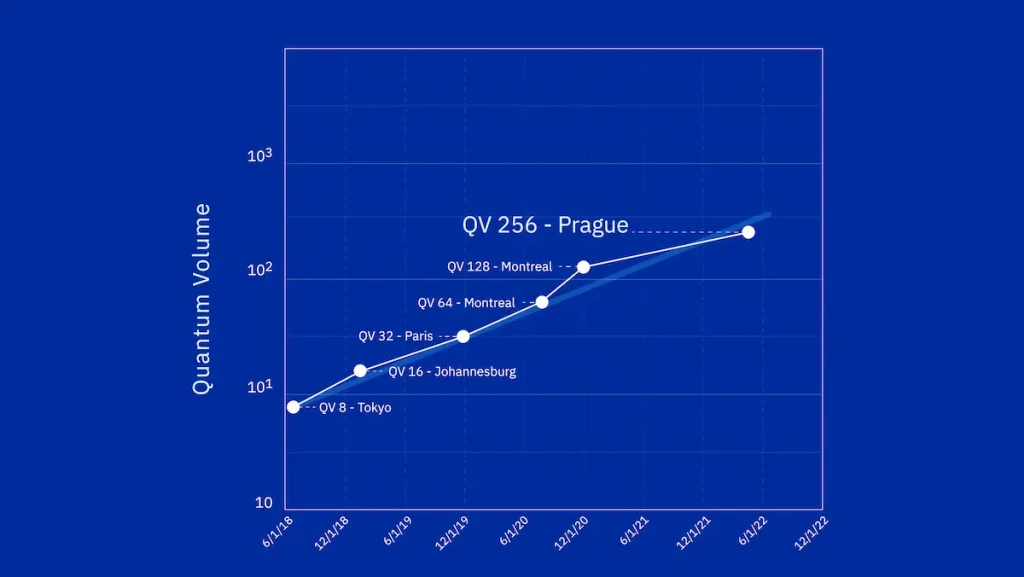
ムーアの法則は量子コンピュータの開発でも適用されるのではないかと言われています。「量子版ムーアの法則」では、1年で2倍のスピードで性能向上が続くと予言されています。IBMでは、2018年のQV8が4年後の2022年にはQV256に成長し、これは4年で32倍になったことを意味します。1年で2.37倍になっているのです。ちなみにQVというのはquantum volumeの略で論理量子ビット数の2乗を示す数値です。量子コンピュータの性能は2のn乗で決まるのでQVに意味があるのか疑問がありますが、もの凄い勢いで伸びていることは実感できると思います。1年で2倍なので、10年で2の10乗=1024倍になります。ああ、20年では1048576倍、つまり100万倍となるのです。
※量子版ムーアの法則、参考サイト