楕円曲線暗号の一方向性

アンドレアス・アントノプロス、マスタリングビットコイン

暗号資産が高騰し、ビットフライヤーやコインチェックなどの暗号通貨取引業者の口座を開設し、ビットコインに投資することは多くの人が行っていますが、ビットコインの仕組みを勉強している人は少ない様です。

https://en.bitcoin.it/wiki/Secp256k1

ビットコインの仕組みは複雑なものですが、最も根本的な仕組みは、Secp256k1 と呼ばれる関数の知識です。それは、$$y^{2}=x^{3}+7 \pmod{2^{256} – 2^{32} – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1}$$

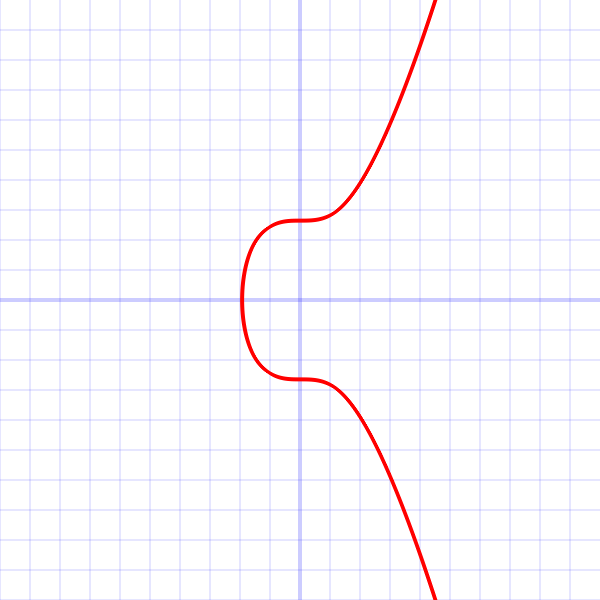
これです！！正確に言えば256ビット有限体上の楕円曲線ということになります。256ビット（10進数で78桁！）の巨大な数で割った余りの世界における楕円曲線です。

$$y=\pm\sqrt{x^{3}+7}$$

両辺の平方根を取るとこんな感じですね。ｙ軸との接点は、$$(0,\pm\sqrt{7})$$

だいたい、$$(0,\pm2.64575)$$くらいになります。

ｙがゼロの場合は、$$(-\sqrt[3]{7},0)$$

だいたい、$$(-1.91293,0)$$くらいになります。

何の変哲もないように見えるこの関数にはスカラー倍算の不可逆性（一方向性）という特別な性質があります。

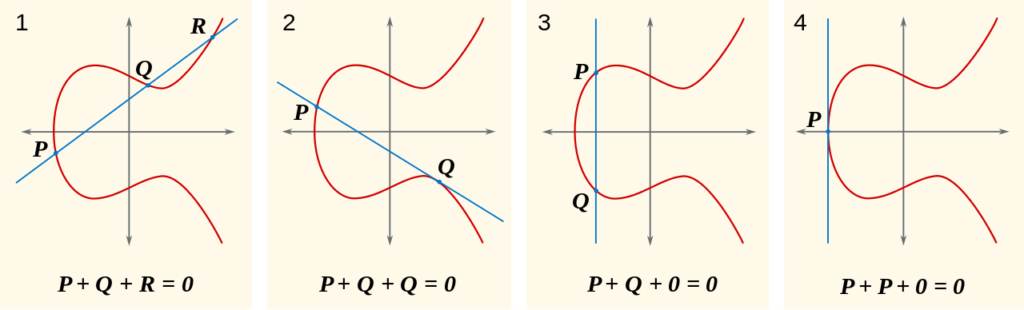
楕円曲線上の点、PとQを通る直線が、楕円曲線上の点Rを通るとき、R(rx,ry)のｘ軸に対する対照点-R(rx,-ry)を、PとQの和であると定義します。

PとQが一致するとき、-R＝２×Pと定義できます。これをスカラー倍算と定義します。2xPにPを足せば3Pということになり、任意の倍数の地点を計算することができます。R=mPの時、スタート地点となるP点とｍを与えればR点を算出することは容易ですが、R点からｍを算出することは極めて困難です。ｍは極めて大きな整数ですが、総当たりで試してみるしかありません。これを楕円曲線離散対数問題と言います。

ちなみに、離散対数問題は、

$$y=x^m$$

のときに、ｙからｍを求める問題です。

この性質は、Rを公開鍵、ｍを秘密鍵とすると、秘密鍵を使えば公開鍵を算出することは容易ですが、公開鍵からは秘密鍵を算出することが極めて困難ということを意味します。この不可逆性（一方向性）を利用してビットコインの安全性は維持されています。

※参考論文

https://www.citp-forum.ipsj.or.jp/wp-content/uploads/2018/09/CITP_report2017_05_akane.pdf

もう少し原始的な一方向性関数（非対称関数）として、素数べきの素因数分解があります。十分大きな素数を２乗した数値を素因数分解せよと言われても、総当たりで膨大な計算をしなければ分解できないが、その素数が分かっていれば２乗の計算は瞬時に行うことができます。

https://en.wikipedia.org/wiki/RSA_Factoring_Challenge

素因数分解の懸賞チャレンジが募集されており、２００桁ぐらいの素因数分解をスパコンで数年かけて計算しています。

例えば、2020年2月に解読された10進数で250桁のRSA250はこのような素因数分解でした。

RSA-250 = 2140324650240744961264423072839333563008614715144755017797754920881418023447140136643345519095804679610992851872470914587687396261921557363047454770520805119056493106687691590019759405693457452230589325976697471681738069364894699871578494975937497937
その素因数分解 =64135289477071580278790190170577389084825014742943447208116859632024532344630238623598752668347708737661925585694639798853367
×33372027594978156556226010605355114227940760344767554666784520987023841729210037080257448673296881877565718986258036932062711

RSA-250の因数分解では、2.1Ghz Intel Xeon Gold 6130 CPUを使用して、約2700CPUコア年が費やされました。１コアで2700年、100コアで27年分の計算量です。ビットコインに使われている楕円曲線暗号の一方向性はこれよりもずっと強度があるというのです。