GPT-3

日経クロステックの「進化がとまらない超人間AI」を読んでみたら、2020年6月にリリースされたGPT-3の話題で持ち切りなんでございます。

どうやらこれは日経コンピューターなどの記事を編集しなおした本のようです。この雑誌は企業などのシステム管理者を対象とする雑誌のようで、普通の大学生や社会人には縁がありません。しかし、超人間AIは人間社会全体を変えてしまうのですから、我々一般人も必読です。

GTP-3(Generative Pretrained Transformer 3)はイーロンマスクが設立したOpenAIが開発した文章作成AIプログラムです。あらかじめ45テラバイト、4100億単語からなるWeb上の文書を学習済みです。自然言語モデルTransformer を改良したものです。

※GPT-3が人類に肉薄しているとのopenAIの報告

https://arxiv.org/pdf/2005.14165.pdf

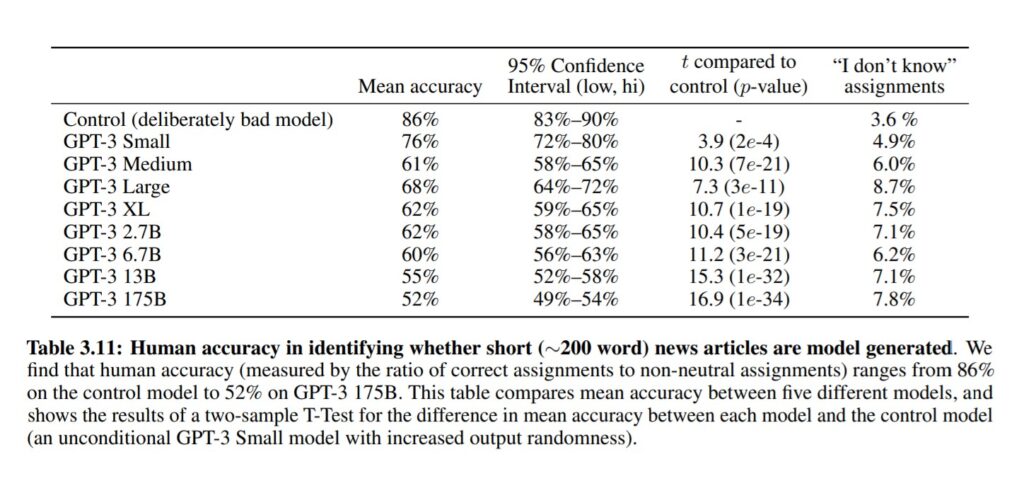
200語未満のfakeニュース記事がAI生成されたかどうかを識別する人間によるテスト。GPT-3に1750億語を読み込ませたモデルでは、人間が人工合成ニュース記事である（つまり人間が書いた記事ではない）と判断できた正答率は52％まで低下し、識別不能と答えた割合が7.8%まで上昇した。完全に識別不能になれば正答率50％になるので、AIによる自然言語理解の完成度は完成目前に達していると言えます。

これはもう、チューリングテストに合格していると言って差し支えないレベルです。

The rate of improvement from original GPT to GPT-3 is impressive. If this rate of improvement continues, GPT-5 or 6 could be indistinguishable from the smartest humans. Just my opinion, not an endorsement. I left OpenAI 2 to 3 years ago. Am a neutral outsider at this point.

— Elon Musk (@elonmusk) August 14, 2020

GTP-3について、イーロンマスクは2020年8月にTwitterで次のように述べています。

『最初のGPTからGPT-3への改善率は印象的です。この改善率が続くとGPT-5または6は最も賢い人間と区別できなくなるだろう。これは私の個人的意見であり、法的に保証するのではありません。私は2から3年前にOpenAIを辞めました。今は中立的な部外者です。』

OpenAI Codex demo 動画。自然言語で話しかけると自動的にプログラムを生成するGPT-3のデモです。

プログラミングが会話によってどんどん進展していく様子は、まるで人間のプログラマーと依頼主が共同作業しているように見えます。驚くべき能力です。イーロンマスクがGPT-5とか6が最も賢い人間と区別がつかないとツイートしたのは、GPT-4とか5で普通の人間と区別がつかないことを意味するのではないかと思ってしまいました。GPT-3のデモはそれを予感させるのに十分な内容です。

※NTTデータの紹介記事

https://www.intellilink.co.jp/column/ai/2021/031700.aspx

こちらの記事によると、GPT-3を利用して偽のブログを作成したところ、GPT-3が書いたものと気づいた人はほとんどいなかったという事例や、GPT-3を使用してネット掲示板に投稿したところ約1週間誰も気づかずにGPT-3と会話をし続けたという事例が報告されています。

リンナはGPT-2のようですが、日本語の会話ができます。

もうアマゾンアレクサとかグーグルホームとかアップルシリの会話レベルとは桁違いの能力に仕上がっています。逆に言いますと、スマホや家庭用の会話AIのレベルも近未来にはこのレベルに到達してしまうということを意味していますね。

※参考動画

「2045年問題 コンピュータが人類を超える日」の松田卓也教授によると、イーロンマスクが「AIに人類が征服されないためにはAI研究は公開でやらなければならない」としてOpenAIの研究が行われてきたが、性能が上がり過ぎて危険だということで逆にソースコードが非公開になってしまったというのです。そしていつのまにかイーロンマスクもOpenAIを辞めたのです。

そのうち、オープンソースのBERTなどでも同様の技術が改良されることでしょう。自然言語処理AIの開発状況は常にウォッチしていく必要があります。

さあ、明日から、学校や職場や家庭で、GPT-3の話題で議論致しましょう！「GPT-3が52%なんだってよ？」と話しかけましょう！

※2023/12/23追記

 ニュートン2023年10月号

ニュートン2023年10月号のCHATGPT特集で、chat-GPT3.5で、各単語のベクトル化（数値化）をするときのパラメーター数（次元数）が、５万２５７次元ベクトルになっているという説明があり驚愕致しました。「鶏肉」とか「フライドチキン」などの単語を、５万個の数値でデータ化しているということになります。

ChatGPTで使われているTransformer、Attention機構では、単語の意味の近さをベクトルの内積を計算することで測っています。

$$ \vec{a} \cdot \vec{b}=a \times b \times  \cos\theta$$