世界で最も美しい等式とされるオイラーの等式
$$e^{i\pi}=-1$$
これは指数関数と三角関数の橋渡しをしている、オイラーの公式のエックスにパイを代入した地点を表現しているのですが、
$$e^{ix}=\cos x+ i\sin x$$
じゃあ、エックスに1を代入したらどうなるのか?
$$e^{i}=\cos 1+ i\sin 1$$
それは、(Google検索窓にe^iと入れてみよう)
$$e^{i}=0.540302306\cdots + 0.841470985\cdots i$$
ただし、
$$e=\lim_{n \to \infty}\Bigl(1+\frac{1}{n}\Bigr)^n=2.71828182846\cdots$$
ネイピア数eは、年率100%の利息=1年後の元利合計200%を半年複利、3か月複利とどんどん細かく複利期間を短くして行った時に、1年後に最大何パーセントまで増やせるかという数値ですね。それは約271.8%なんですね。元本100%を差し引くと、元々の利率100%が171.8%になるのですから「複利は最大で単利の1.718倍になる」というのがジョン・ネイピアの発見なんですね。
なんとも不思議な数値です。ちなみに、
$$1^{i}= 1$$
なんだそうです。1を何回かけても1というわけです。その他、0.99^iとか1.01^iとかもgoogle先生に聞いてみると面白いですよ。
オイラーの公式の厳密な導出とか証明とかテイラー展開などは市販の本を読んで頂くとして、この記事では雰囲気を掴んで頂きたいと思います。それは、指数関数がぐるぐると回転しているということでございます。
$$i^2=-1$$
これはみんな知ってる虚数の定義ですが、この次が大事なんですね、
$$i^3=-i$$
うーん、なんの変哲もない、当たり前の式ですが!
次の、これが一番大事な数式、
$$i^4=1$$
がーん!またも当たり前の計算ですが、2乗でマイナス1になるというよりも、4乗して1になるということの方が虚数の重要な性質であると気づきました!
$$i^5=i$$
はい、iのn乗は周期関数になっているのですね。複素平面上をぐるぐる回っているわけです。
つまり、指数関数がぐるぐる回ってるわけではなく、「複素平面における指数関数はぐるぐる回っている」ということに気付かされました。
これが、オイラーの公式を分かった、ということの意味なのでしょうか。これが分かったからと言ってシンギュラリティを乗り越えられるわけではありませんね。でも、分かろうとして進んでいく姿勢が大事なのだと思います。未知のことに好奇心を持ってぶつかっていく「分からないことを勉強する姿勢」が大事です。
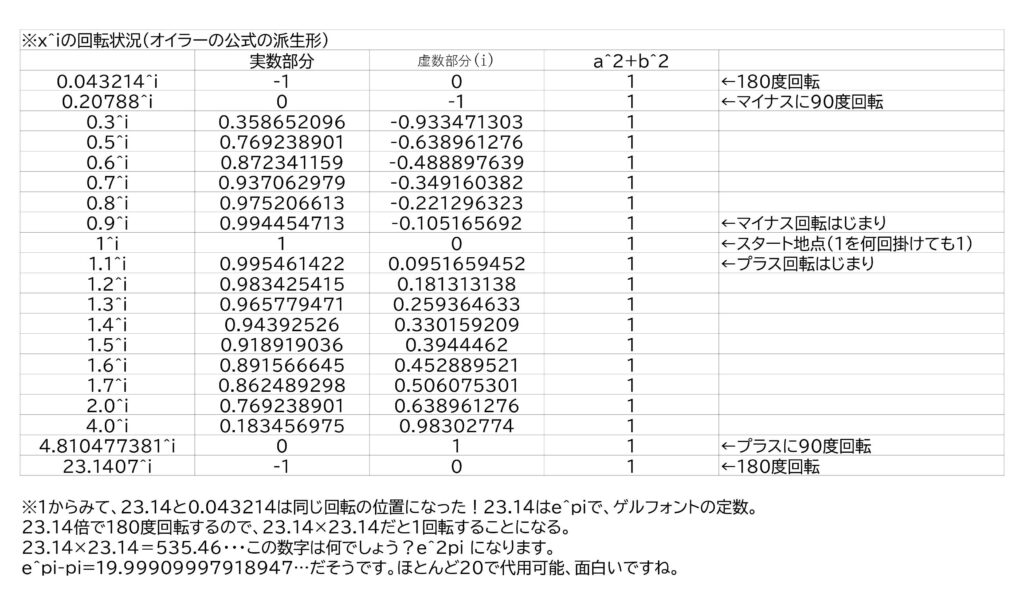
※おまけ(ゲルフォントの定数)
※参考記事
https://sci-tech.ksc.kwansei.ac.jp/~shimeno/math/euler/euler.pdf
※参考書籍




コメントを残す